Quadrilaterals

Question 1.
State whether the statements are true or false.

• i) Every parallelogram is a trapezium.
• ii) All parallelograms are quadrilaterals.
• iii) All trapeziums are parallelograms.
• iv) A square is a rhombus.
• v) Every rhombus is a square.
• vi) All parallelograms are rectangles.

Solution:

• i) True
• ii) True
• iii) False
• iv) True
• v) False
• vi) False

Question 2.
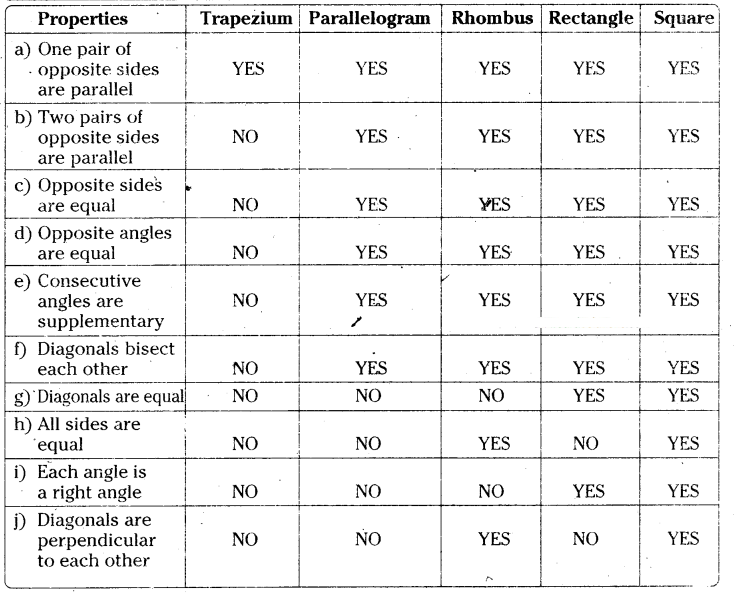
Complete the following table by writing YES if the property holds for the particular quadrilateral and NO if property does not holds.

Solution

Question 3.
ABCD is a trapezium in which AB ‖ CD. If AD = BC, show that ∠A = ∠B and ∠C = ∠D.

Solution:
Given that in □ABCD AB ‖ CD; AD = BC
Mark a point ‘E’ on AB such DC = AE.

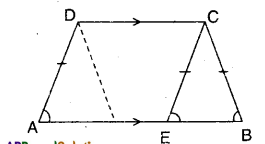
Join E, C.
Now in AECD quadrilateral
AE // DC and AE = DC
∴ □AECD is a parallelogram.
∴ AD//EC
∠DAE = ∠CEB (corresponding angles) ……………..(1)
In ΔCEB; CE = CB (∵ CE = AD)
∴ ∠CEB = ∠CBE (angles opp. to equal sides) …………….. (2)
From (1) & (2)
∠DAE = ∠CBE
⇒ ∠A = ∠B
Also ∠D = ∠AEC (∵ Opp. angles of a parallelogram)
= ∠ECB + ∠CBE [ ∵ ∠AEC is ext. angle of ΔBCE] |
= ∠ECB + ∠CEB [ ∵∠CBE = ∠CEB]
= ∠ECB + ∠ECD [∵ ∠ECD = ∠CEB alt. int. angles]
= ∠BCD = ∠C
∴ ∠C = ∠D

Question 4.
The four angles of a quadrilateral are in the ratio of 1 : 2 : 3 : 4. Find the measure of each angle of the quadri-lateral.

Solution:
Given that, the ratio of angles of a quad-rilateral = 1 : 2 : 3 : 4
Sum of the terms of the ratio
= 1 +2 + 3 + 4= 10
Sum of the four interior angles of a quadrilateral = 360°
∴ The measure of first angle

Question 5.
ABCD is a rectangle, AC is diagonal. Find the angles of ΔACD. Give reasons.

Solution:

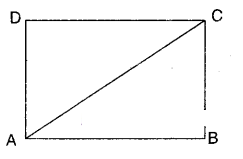
Given that □ABCD is a rectangle;
AC is its diagonal.
In ΔACD; ∠D = 90° [ ∵ ∠D is also angle of the rectangle]
∠A + ∠C = 90° [ ∵ ∠D = 90° ⇒ ∠A + ∠C = 180°-90° = 90°]
(i.e,,) ∠D right angle and
∠A, ∠C are complementary angles.

Question 1.
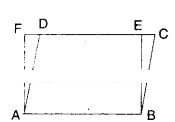
In the given figure ABCD is a parallelogram. ABEF is a rectangle. Show that ΔAFD ≅ ΔBEC

Solution:
Given that □ABCD is a parallelogram.
□ABEF is a rectangle.
In ΔAFD and ΔBEC
AF = BE ( ∵ opp. sides of rectangle □ABEF)
AD = BC (∵ opp. sides of //gm □ABCD)
DF = CE (∵ AB = DC = DE + EC , AB = EF = DE + DF)
∴ ΔAFD ≅ ΔBEC (SSS congruence)

Question 2.
Show that the diagonals of a rhombus divide it into four congruent triangles.

Solution:

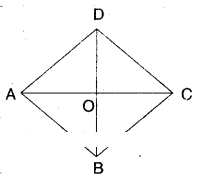
□ABCD is a rhombus.
Let AC and BD meet at O.
In ΔAOB and ΔCOD
∠OAB = ∠OCD (alt.int. angles)
AB = CD (def. of rhombus)
∠OBA = ∠ODC ........(1) (alt. int. angles)
∴ ΔAOB ≅ ΔCOD (ASA congruence)
Thus AO = OC (CPCT)
Also ΔAOD ≅ ΔCOD ......(2)
[ ∵ AO = OC; AD = CD; OD = OD SSS congruence]
Similarly we can prove
ΔAOD ≅ ΔCOB ...... (3)
From (1), (2) and (3) we have
ΔAOB ≅ ΔBOC ≅ ΔCOD ≅ ΔAOD
∴ Diagonals of a rhombus divide it into four congruent triangles.

Question 3.
In a quadrilateral ABCD, the bisector of ∠C and ∠D intersect at O. Prove that ∠COD = 1/2 (∠A + ∠B) .
(OR)
In a quadrilateral ABCD, the bisectors of ∠A and ∠B are intersects at ‘O’ then prove that ∠AOB = 1/2 (∠C + ∠D)

Solution:

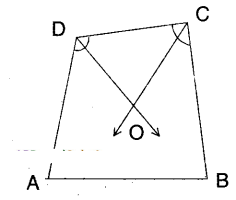
In a quadrilateral □ABCD
∠A + ∠B + ∠C + ∠D = 360°
(angle sum property)
∠C + ∠D = 360° - (∠A + ∠B)
1/2 (∠C + ∠D) = 180 - 1/2 (∠A + ∠B) ...... (1)
(∵ dividing both sides by 2) .
But in ΔCOD
1/2∠C + 1/2 ∠D + ∠COD = 180°
1/2∠C + 1/2 ∠D = 180° - ∠COD
∴12(∠C +∠D) = 180° -∠COD.....(2)
From (1) and (2);
180° - ∠COD = 180° - 1/2 (∠A + ∠B)
∴ ∠COD = 1/2 (∠A + ∠B)
Hence proved.

Question 1.
The opposite angles of a parallelogram are (3x - 2)° and (x + 48)°. Find the measure of each angle of the parallelogram.

Solution:
Given that the opposite angles of a parallelogram are (3x - 2)° and (x + 48)°
Thus 3x – 2 = x + 48
(∵ opp. angles of a //gm are equal)
3x - x = 48 + 2
2x = 50
x = 50/2 = 25°
∴ The given angles are (3 x 25 - 2)° and (25 + 48) °
= (75 - 2)° and 73° = 73° and 73°
We know the consecutive angles are supplementary.
∴ The other two angles are (180°-73°) and (180°-73°)
= 107° and 107°
∴ The four angles are 73°, 107°, 73° and 107°.

Question 2.
Find the measure of all the angles of a parallelogram, if one angle is 24° less than the twice of the smallest angle.

Solution:
Let the smallest angle = x
Then its consecutive angle = 180 - x°
By problem (180 - x)° = (2x- 24)°
(∵ opp. angles are equal)
180 + 24 = 2x + x
3x = 204
x =204/3 = 68°
∴ The angles are
68°; (2 x 68 - 24)°; 68°; (2 x 68 - 24)°
= 68°, 112°, 68°, 112°

Question 3.
In the given figure ABCD is a paral-lelogram and E is the mid point of the side BC. If DE and AB are produced to meet at F, show that AF = 2AB.

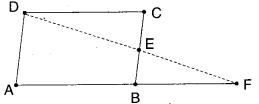
Solution

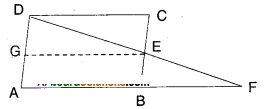
Given that □ABCD is a parallelogram.
E is the midpoint of BC.
Let G be the midpoint of AD.
Join G, E.
Now in ΔAFD, GE is the line joining the midpoints G, E of two sides AD and FD.
∴GE // AF and GE = 1/2 AF
But GE = AB [ ∵ ABEG is a parallelo¬gram and AB, GE forms a pair of opp. sides]
12 = AB ⇒ AF = 2AB
Hence Proved.

Question 4.
In the given figure ABCD is a paral¬lelogram. P, Q are the midpoints of sides AB and DC

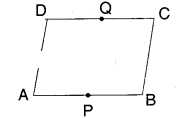
respectively. Show that

Solution

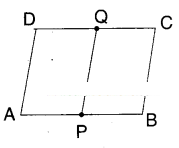
□ABCD is a parallelogram.
P, Q are the mid points of AB and CD.
Join Q, P.
Now AB = CD (Opp. sides of a //gm)
12AB = 12CD
PB = QC
Also PB // QC.
Now in □PBCQ;
PB = QC; PB//QC
Hence □PBCQ is a parallelogram.

Question 5.
ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle QAC and CD//BA as shown in the figure. Show that i) ∠DAC = ∠BCA

ii) ABCD is a parallelogram.

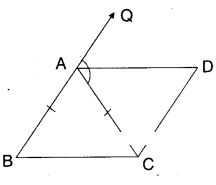
Solution:
Given that AABC is isosceles; AB = AC
AD is bisector of ∠QAC
i) In ΔABC, AB = AC ⇒ ∠B = ∠ACB
(angles opp. to equal sides)
Also ∠QAC = ∠B + ∠ACB
∠QAC = ∠BCA + ∠BCA
(∵∠BCA = ∠B)
⇒ 1/2∠QAC = 1/2 [2 ∠BCA]
⇒ ∠DAC = ∠BCA [ ∵ AD is bisector of ∠QAC]

ii) From (i) ∠DAC = ∠BCA
But these forms a pair of alt. int. angles for the pair of lines AD and BC; AC as a transversal.
∴ AD//BC
In □ABCD ; AB // DC; BC // AD
□ABCD is a parallelogram.

Question 6.
ABCD is a parallelogram AP and CQ are perpendiculars drawn from vertices A and C on diagonal BD (see figure). Show that 1) ΔAPB ≅ ΔCQD ii) AP = CQ.

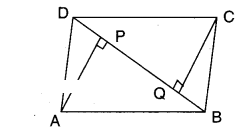
Solution:
Given that □ABCD is a parallelogram.
BD is a diagonal.
AP ⊥ BD and CQ ⊥ BD
i) In ΔAPB and ΔCQD
AB = CD ( ∵ Opp. sides of //gm ABCD)
∠APB = ∠CQD (each 90°)
∠PBA = ∠QDC (alt. int. angles for the lines AB and DC)
∴ ΔAPB ≅ ΔCQD (AAS congruence)

ii) From (1) ΔAPB ≅ ΔCQD
⇒ AP = CQ (CPCT)

Question 7.
In Δs ABC and Δs DEF, AB = DC and AB//DE; BC = EF and BC//EF. Vertices A, B and C are joined to vertices D, E and F respectively (see figure). Show that

• i) ABED is a parallelogram
• ii) BCFE is a parallelogram
• iii) AC = DF
• iv) ΔABC = ΔDEF

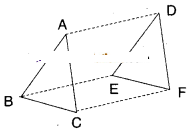
Solution

Given that in ΔABC and ΔDEF
AB = DE and AB // DE
BC = EF and BC//EF.
i) In □ABED AB//ED and AB = ED
Hence □ABED is a parallelogram.

ii) In □BCFE; BC = EF and BC//EF
Hence □BCFE is a parallelogram.

iii) ACFD is a parallelogram (In a paral-lelogram opposite sides are equal).
So, AC = DF.

iv) Consider ΔABC = ΔDEF
AB = DE (given);
AC = DF (proved)
BC = EF (given)
∴ ΔABC ≅ ΔDEF (SSS congruency rule).

Question 8.
ABCD is a parallelogram. AC and BD are the diagonals intersect at ‘O’. P and Q are the points of trisection of the diagonal BD. Prove that CQ//AP and also AC bisects PQ.

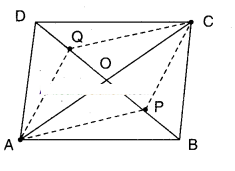
Solution:
Given □ABCD is a parallelogram;
BD is a diagonal.
P, Q are the points of trisection of BD.
In ΔAPB and ΔCQD
AB = CD (... Opp. sides of //gm ABCD)
BP = DQ (given)
∠ABP = ∠CDQ (alt. int. angles for the lines AB//DC, BD as a transversal)
ΔAPB = ΔCQD (SAS congruence)
Similarly in ΔAQD and ΔCPB
AD = BC (opp. sides of //gm ABCD)
DQ = BP (given)
∠ADQ = ∠CBP (all int. angles for the lines AD//BC, BD as a transversal)
ΔAQD ≅ ΔCPB
Now in □APCQ
AP = CQ (CPCT of AAPB, ACQD)
AQ = CP (CPCT of AAQD and ACPB)
∴ □APCQ is a parallelogram.
∴ CQ//AP (opp. sides of//gm APCQ)
Also AC bisects PQ. [ ∵ diagonals of //gm APCQ]

Question 9.
ABCD is a square. E, F, G and H are the mid points of AB, BC, CD and DA respectively. Such that AE = BF = CG = DH. Prove that EFGH is a square.

Solution:

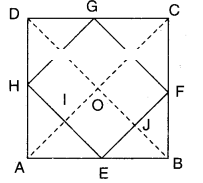
Given that ABCD is a square.
E, F, G, H are the mid points of AB, BC, CD and DA.
Also AE = BF = CG = DH
In ΔABC; E, F are the mid points of sides AB and BC.
∴ EF//AC and EF = 1/2 AC
Similarly GH//AC and GH = AC
GF//BD and GF = 1/2 BD
HE//BD and HE = 1/2 BD

But AC = BD (∵ diagonals of a square)
∴ EF = FG = GH = HE
Hence EFGH is a rhombus.
Also AC ⊥ BD
(∵ diagonals of a rhombus)
∴ In //gm OIEJ [ ∵ 0I // EJ; IE // OJ]
We have ∠IOJ = ∠E
[ ∵ Opp. angles of a //gm]
∴ ∠E - 90°
Hence in quad. EFGH; all sides are equal and one angle is 90°.
∴ EFGH is a square.

Question 1.
ABC is a triangle. D is a point on AB such that AD =1/4 AB and E is a point on AC such that AE =1/4 AC. If DE = 2 cm find BC.

Solution:

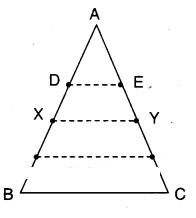
Given that D and E are points on AB and AC.
Such that AD = 1/4 AB and AE = 1/4 AC
Let X, Y be midpoints of AB and AC.
Joint D, E and X, Y.
Now in ΔAXY; D, E are the midpoints of sides AX and AY.
∴ DE // XY and DE = 1/2 XY
⇒ 2 cm = 1/2 XY
⇒ XY = 2 x 2 = 4cm
Also in ΔABC; X, Y are the midpoints of AB and AC.
∴ XY//BC and XY = 1/2 BC
4 cm = 1/2 BC
⇒ BC = 4 x 2 = 8 cm

Question 2.
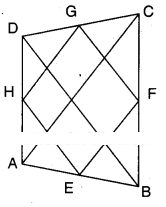
ABCD is a quadrilateral. E, F, G and H are the midpoints of AB, BC, CD and DA respectively. Prove that EFGH is a parallelogram.

Solution:
Given that E, F, G and H are the midpoints of the sides of quad. ABCD.
In ΔABC; E, F are the midpoints of the sides AB and BC.
∴ EF//AC and EF = 1/2 AC
Also in ΔACD; HG // AC
and HG = 1/2 AC
∴ EF // HG and EF = HG
Now in □EFGH; EF = HG and EF // HG
∴ □EFGH is a parallelogram.

Question 3.
Show that the figure formed by joining the midpoints of sides of a rhom¬bus successively is a rectangle.

Solution:

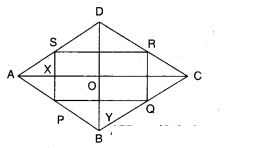
Let □ABCD be a rhombus.
P, Q, R and S be the midpoints of sides of □ABCD
In ΔABC,
P, Q are the midpoints of AB and BC.
∴ PQ//AC and PQ = 1/2 AC .........(1)
Also in ΔADC, ,
S, R are the midpoints of AD and CD.
∴ SR//AC and SR = 1/2 AC ......(2)
From (1) and (2);
PQ // SR and PQ = SR
Similarly QR // PS and QR = PS
∴ □PQRS is a parallelogram.
As the diagonals of a rhombus bisect at right angles.
∠AOB - 90°
∴ ∠P = ∠AOB = 90°
[opp. angles of //gm PYOX] Hence □PQRS is a rectangle as both pairs of opp. sides are equal and parallel, one angle being 90°.

Question 4.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and DC respectively. Show that the line segments AF and EC trisect the diagonal BD.

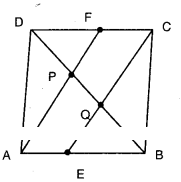
Solution:
□ABCD is a parallelogram. E and F are the mid points of AB and CD.
∴ AE = 12AB and CF = 12CD
Thus AE = CF [∵ AB - CD]
Now in □AECF, AE = CF and AE ‖CF
Thus □AECF is a parallelogram.
Now in ΔEQB and ΔFDP
EB = FD [Half of equal sides of a //gm]
∠EBQ = ∠FDP[alt. int.angles of EB//FD]
∠QEB = ∠PFD
[∵∠QED = ∠QCF = ∠PFD]
∴ ΔEQB ≅ ΔFPD [A.S.A. congruence]
∴ BQ = DP [CPCT] ...... (1)
Now in ΔDQC; PF // QC and F is the midpoint of DC.
Hence P must be the midpoint of DQ
Thus DP = PQ ....... (2)
From (1) and (2), DP = PQ = QB
Hence AF and CE trisect the diagonal BD.

Question 5.
Show that the line segments joining the mid points of the opposite sides of a quadrilateral and bisect each other.

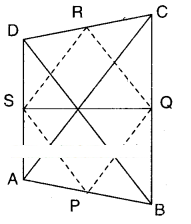
Solution:
Let ABCD be a quadrilateral.
P, Q, R, S are the midpoints of sides of □ABCD.
Join (P, Q), (Q, R), (R, S) and (S, P).
In ΔABC; P, Q are the midpoints of AB and BC.
∴ PQ // AC and PQ = 1/2 AC .....(1)
Also from ΔADC
S, R are the midpoints of AD and CD
SR // AC and SR = 1/2 AC .......(2)
∴ From (1) & (2)
PQ = SR and PQ //SR
∴ □PQRS is a parallelogram.
Now PR and QS are the diagonals of □ PQRS.
∴ PR and QS bisect each other.

Question 6.
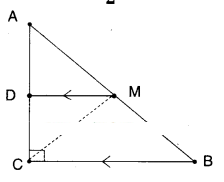
ABC is a triangle right angled at’C’. A line through the midpoint M of hypotenuse AB and parallel to BC intersects AC at D. Show that

• i) D is the midpoint of AC
• ii) MD ⊥ AC
• iii) CM = MA=1/2 AB

Solution

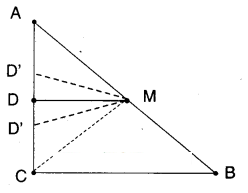
Given that in ΔABC; ∠C = 90°
M is the midpoint of AB.
i) If ‘D’ is the midpoints of AC.
The proof is trivial.
Let us suppose D is not the mid point of AC.
Then there exists D’ such that AD’ = D’C
Then D’M is a line parallel to BC through M.
Also DM is a line parallel to BC through M.
There exist two lines parallel to same line through a point M.
This is a contradiction.
There exists only one line parallel to a given line through a point not on the line.
∴ D’ must coincides with D
∴ D is the midpoint of AC

ii) From (i) DM // BC
Thus ∠ADM = ∠ACB = 90°
[corresponding angles]
⇒ MD ⊥ AC

iii) In ΔADM and ΔCDM
AD = CD [ ∵ D is midpoint from (i)]
∠ADM = ∠MDC (∵ 90° each)
DM = DM (Common side)
∴ ∠ADM = ∠CDM (SAS congruence)
⇒ CM = MA (CPCT)
CM = 1/2 AB (∵ M is the midpoint of AB)
∴ CM = MA = 1/2 AB